第一届北京大学信息安全综合能力竞赛个人题解
签到
题目内容是一个 pdf 文件,用 Adobe Acrobat 打开,看到其中包含一些特殊符号。
在编辑模式下,查看得到其字体为 Wingdings,这是一个装饰字体,文本内容其实是 ASCII 码。文本范围是超出页面的,resize 之后复制出其内容,给出了两行文字:1
2fa{aeAGetTm@ekaev!
lgHv__ra_ieGeGm_1}
这是栅栏密码,得到 flag 为flag{Have_A_Great_Time@GeekGame_v1!}。
小北问答 Remake
北京大学燕园校区有理科 1 号楼到理科 X 号楼,但没有理科 (X + 1) 号及之后的楼。X 是?
在 Google Earth 中搜索,存在理科 5 号楼,但没有理科 6 号楼。故答案为 5。
上一届(第零届)比赛的总注册人数有多少?
在北京大学新闻网中找到报道北京大学举办首届信息安全综合能力竞赛,得到「本次大赛共有 407 人注册参赛」,故答案为 407。
geekgame.pku.edu.cn 的 HTTPS 证书曾有一次忘记续期了,发生过期的时间是?
搜索「ssl cert database」,找到网站crt.sh。在该网站上搜索 geekgame.pku.edu.cn,并根据题目给出的正则表达式寻找过期时间秒数以 3 结尾的证书,得到证书 4362003382。其过期时间为 Jul 11 00:49:53 2021 GMT,将时区换为 UTC + 8,得到 2021-07-11T08:49:53 + 08:00。
2020 年 DEFCON CTF 资格赛签到题的 flag 是?
找到 2020 年 DEFCON CTF 资格赛的网站是OOO DEF CON CTF Quals,打开第一题 welcome-to-dc2020-quals,下载 welcome.txt,获得 flag 为
OOO{this_is_the_welcome_flag}。在大小为 672328094 * 386900246 的方形棋盘上放 3 枚(相同的)皇后且它们互不攻击,有几种方法?
在The On-Line Encyclopedia of Integer Sequences 中搜索「3 queens」,没有直接找到
的通解,但有一篇相关的文章 Number of ways to place 3 nonattacking queens on an n X n board.。里面给出了通解的表达式: 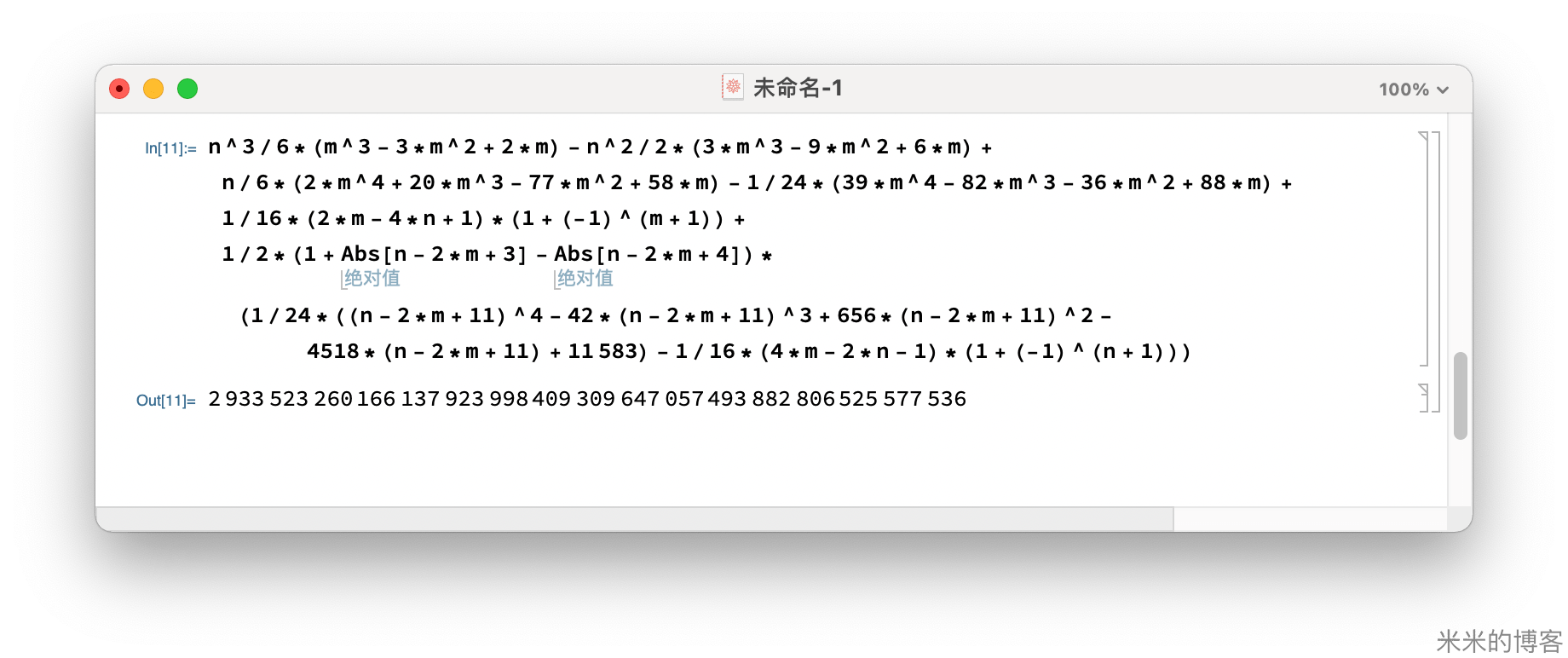
代入数据计算得 2933523260166137923998409309647057493882806525577536。这里直接用 Mathematica 计算了。
上一届(第零届)比赛的 “小北问答 1202” 题目会把所有选手提交的答案存到 SQLite 数据库的一个表中,这个表名叫?
在第零届比赛的 GitHub 仓库geekgame-0th 中查找,在src/choice/game/db.py 中得到表名叫 submits。
国际互联网由许多个自治系统(AS)组成。北京大学有一个自己的自治系统,它的编号是?
在中国 AS 自治系统号码中查找 Peking University,找到编号 AS59201。另一个搜索结果 CNGI - BJ-IX3-AS-AP CERNET2 IX at Peking University, CN 不是正确答案。
截止到 2021 年 6 月 1 日,完全由北京大学信息科学技术学院下属的中文名称最长的实验室叫?
在信息科学技术学院 2021 年招生指南中找名字最长的实验室,为「区域光纤通信网与新型光通信系统国家重点实验室」。
